B树和B+树的插入、删除图文详解

一.B树

1.B树的定义

B树也称B-树,它是一颗多路平衡查找树。
我们描述一颗B树时需要指定它的阶数，阶数表示了一个结点最多有多少个孩子结点，一般用字母m表示阶数。
当m取2时，就是我们常见的二叉搜索树。

一颗m阶的B树定义如下：
    1）每个结点最多有m-1个关键字。
    2）根结点最少可以只有1个关键字。
    3）非根结点至少有Math.ceil(m/2)-1个关键字。
    4）每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它。
    5）所有叶子结点都位于同一层，或者说根结点到每个叶子结点的长度都相同。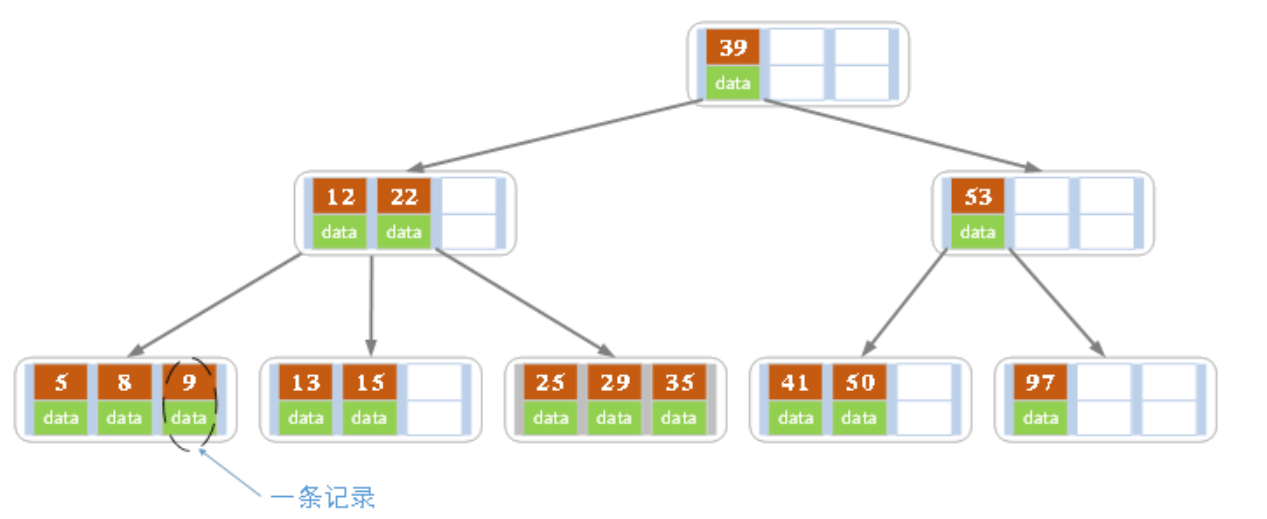

上图是一颗阶数为4的B树。

(1).在实际应用中的B树的阶数m都非常大（通常大于100），所以即使存储大量的数据，B树的高度仍然比较小。
(2).每个结点中存储了关键字（key）和关键字对应的数据（data），以及孩子结点的指针。
(3).我们将一个key和其对应的data称为一个记录。但为了方便描述，除非特别说明，后续文中就用key来代替（key, value）键值对这个整体。
(4).在数据库中我们将B树（和B+树）作为索引结构，可以加快查询速速，此时B树中的key就表示键，而data表示了这个键对应的条目在硬盘上的逻辑地址。

2.B树的插入操作

插入操作是指插入一条记录，即（key, value）的键值对。如果B树中已存在需要插入的键值对，则用需要插入的value替换旧的value。
若B树不存在这个key,则一定是在叶子结点中进行插入操作。
    1）根据要插入的key的值，找到叶子结点并插入。
    2）判断当前结点key的个数是否小于等于m-1，若满足则结束，否则进行第3步。
    3）以结点中间的key为中心分裂成左右两部分，然后将这个中间的key插入到父结点中，
       这个key的左子树指向分裂后的左半部分，这个key的右子支指向分裂后的右半部分，然后将当前结点指向父结点，继续进行第3步。

下面以5阶B树为例，介绍B树的插入操作，在5阶B树中，结点最多有4个key,最少有2个key

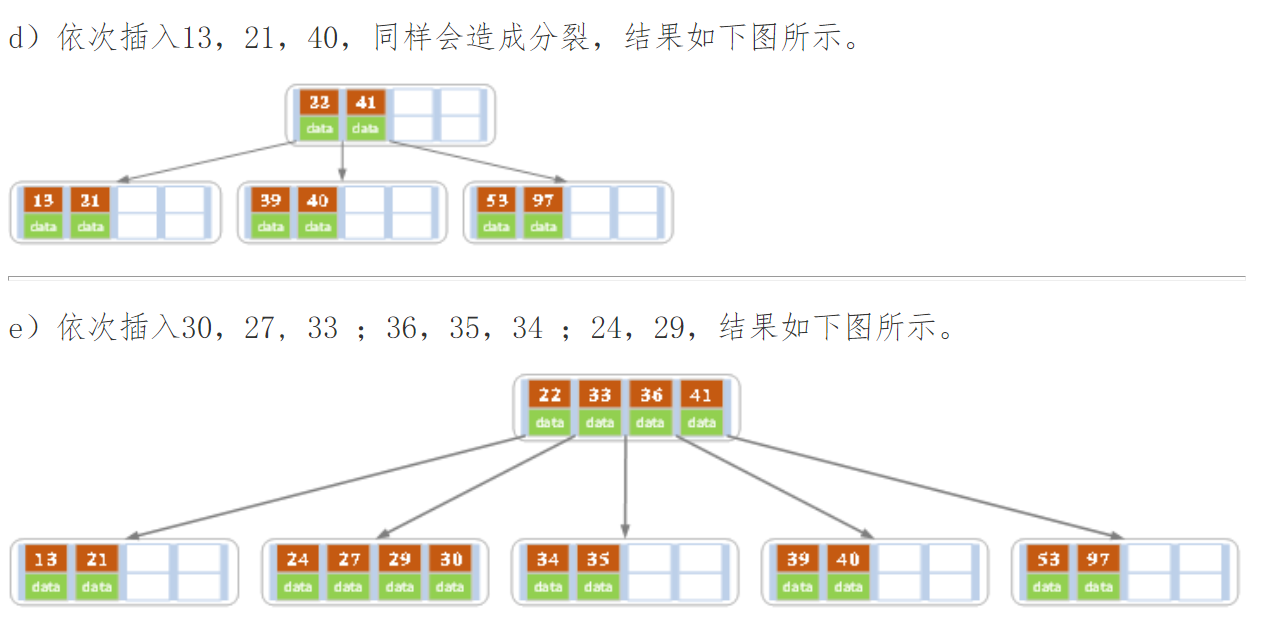
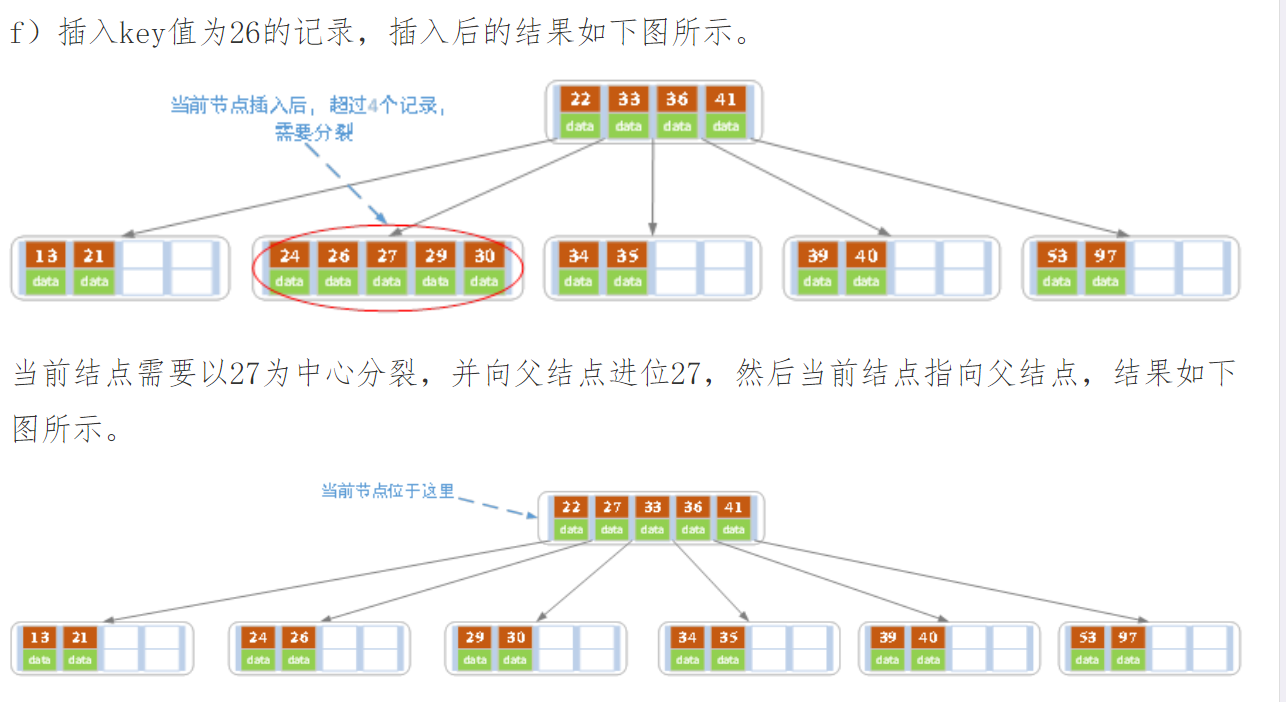
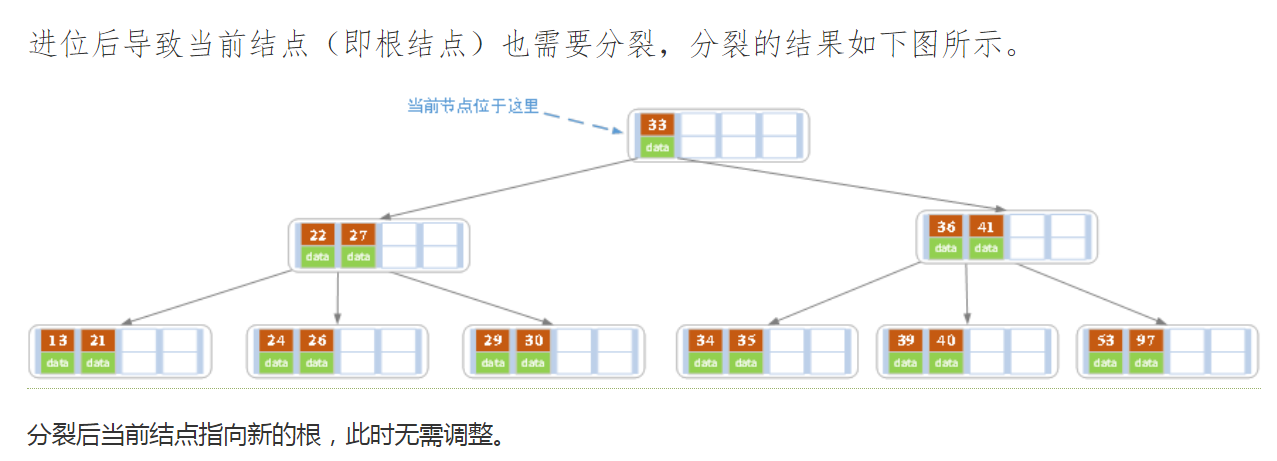
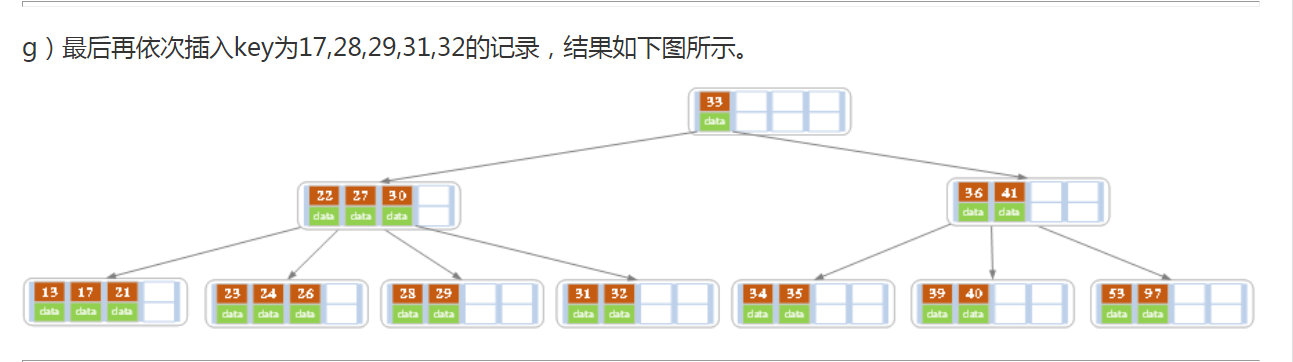
在实现B树的代码中，为了使代码编写更加容易，将结点中存储记录的数组长度定义为m而非m-1，
方便底层的结点由于分裂向上层插入一个记录时，上层有多余的位置存储这个记录。

同时，每个结点还可以存储它的父结点的引用，这样就不必编写递归程序。

一般来说，对于确定的m和确定类型的记录，结点大小是固定的，无论它实际存储了多少个记录。但是分配固定结点大小的方法会存在浪费的情况，
比如key为28,29所在的结点，还有2个key的位置没有使用，但是已经不可能继续在插入任何值了，因为这个结点的前序key是27,后继key是30,所有整数值都用完了。

如果记录先按key的大小排好序，再插入到B树中，结点的使用率就会很低，最差情况下使用率仅为50%。

3.B树的删除操作

删除操作是指，根据key删除记录，如果B树中的记录中不存对应key的记录，则删除失败。
    1）如果当前需要删除的key位于非叶子结点上，则用后继key（后继记录）覆盖要删除的key，然后在后继key所在的子支中删除该后继key。
       此时后继key一定位于叶子结点上，这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步
    2）该结点key个数大于等于Math.ceil(m/2)-1，结束删除操作，否则执行第3步。
    3）如果兄弟结点key个数大于Math.ceil(m/2)-1，则父结点中的key下移到该结点，兄弟结点中的一个key上移，删除操作结束。

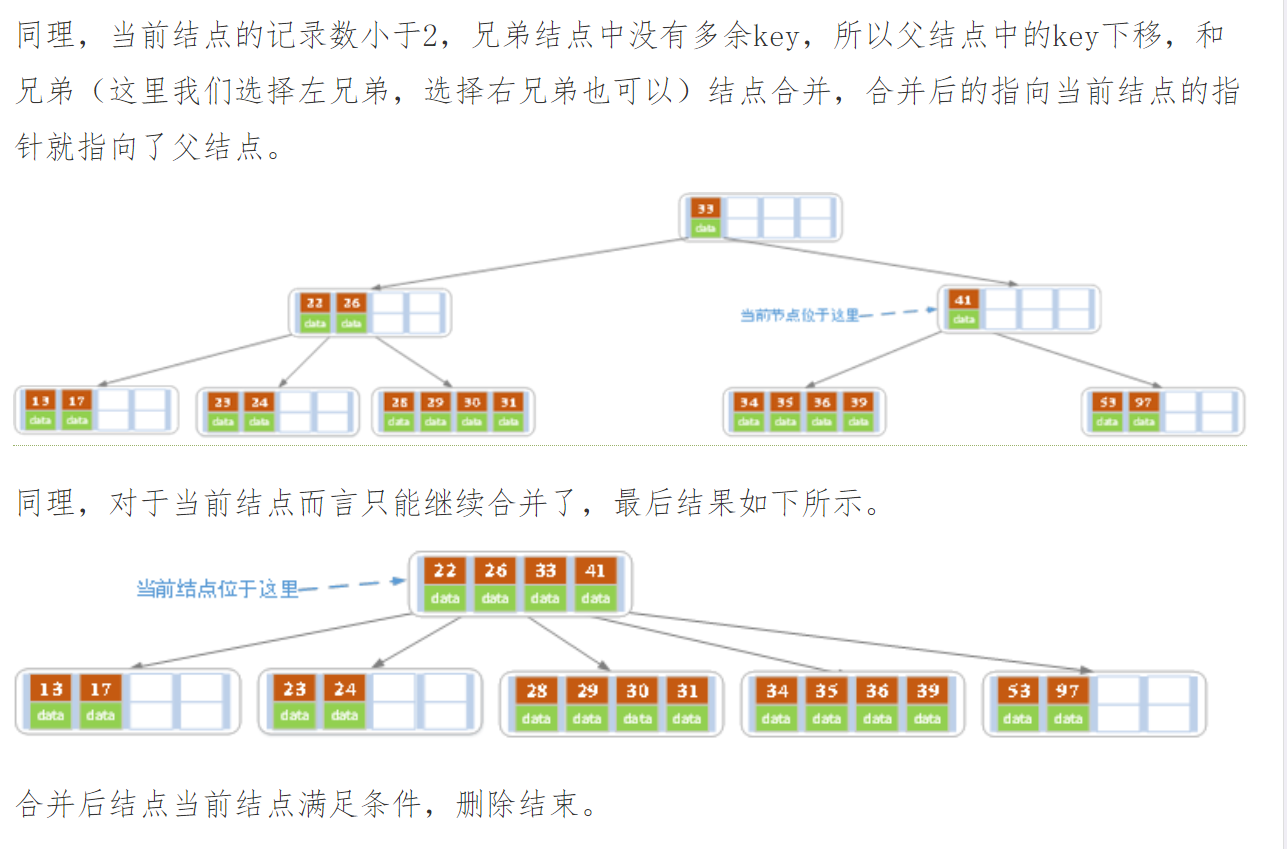
    否则，将父结点中的key下移与当前结点及它的兄弟结点中的key合并，形成一个新的结点。
    原父结点中的key的两个孩子指针就变成了一个孩子指针，指向这个新结点。然后当前结点的指针指向父结点，重复上第2步。
    有些结点它可能即有左兄弟，又有右兄弟，那么我们任意选择一个兄弟结点进行操作即可。

下面以5阶B树为例，介绍B树的删除操作，5阶B树中，结点最多有4个key,最少有2个key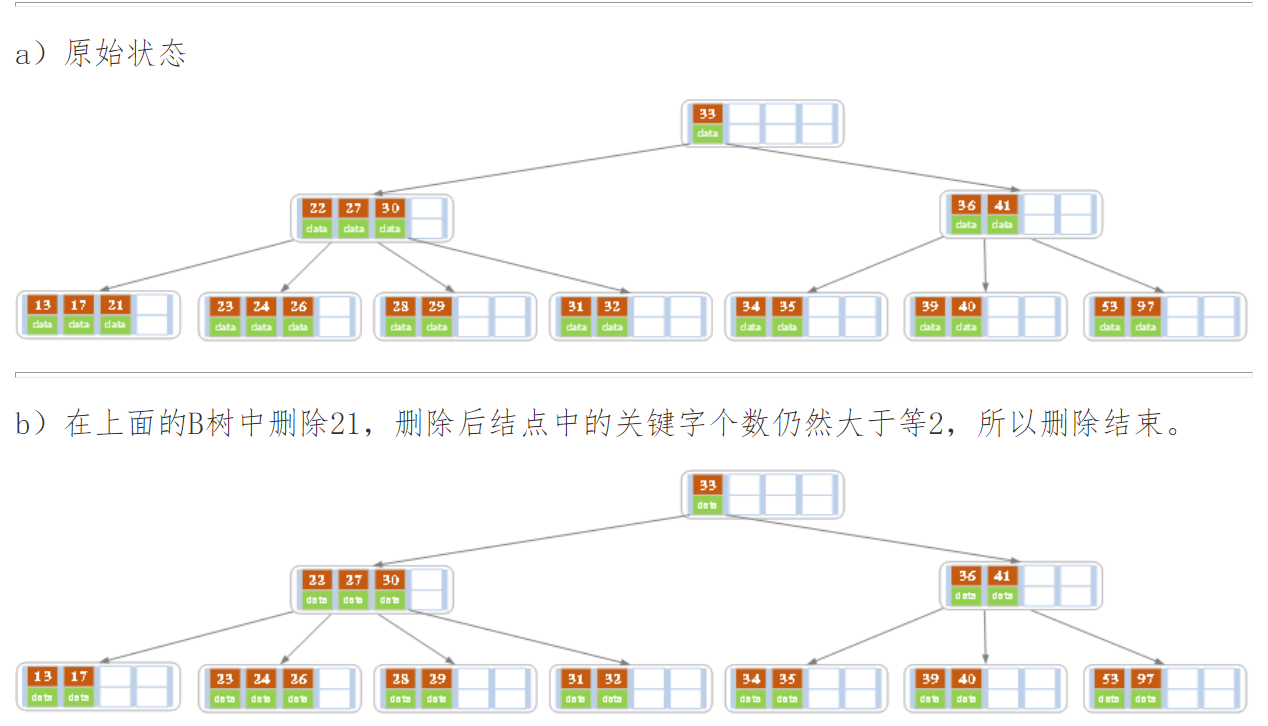

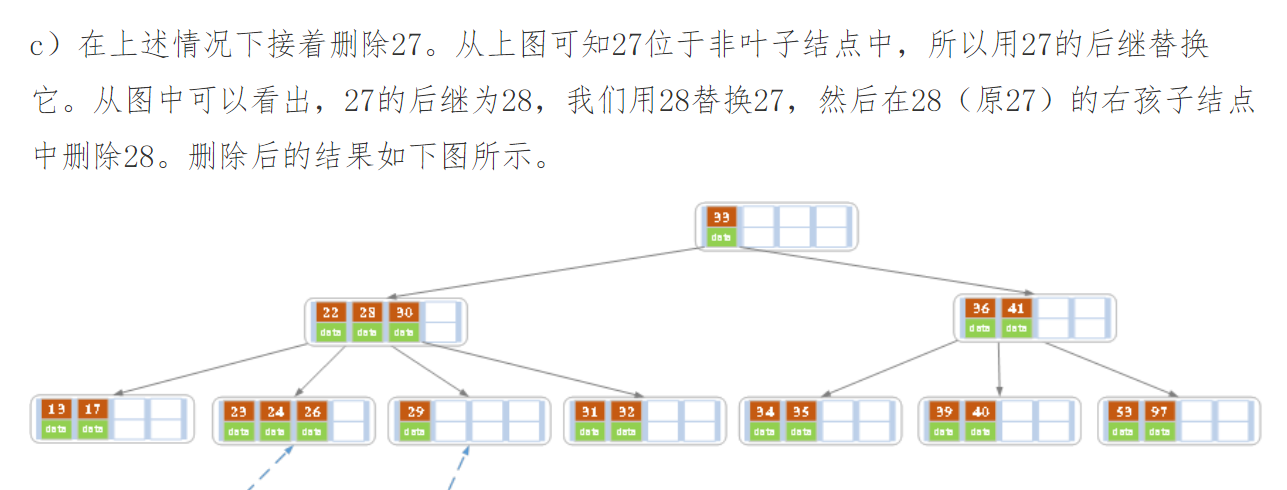
删除后发现，当前叶子结点的记录的个数小于2，而它的兄弟结点中有3个记录
（当前结点还有一个右兄弟，选择右兄弟就会出现合并结点的情况，不论选哪一个都行，只是最后B树的形态会不一样而已），
我们可以从兄弟结点中借取一个key。所以父结点中的28下移，兄弟结点中的26上移,删除结束。
结果如下图所示。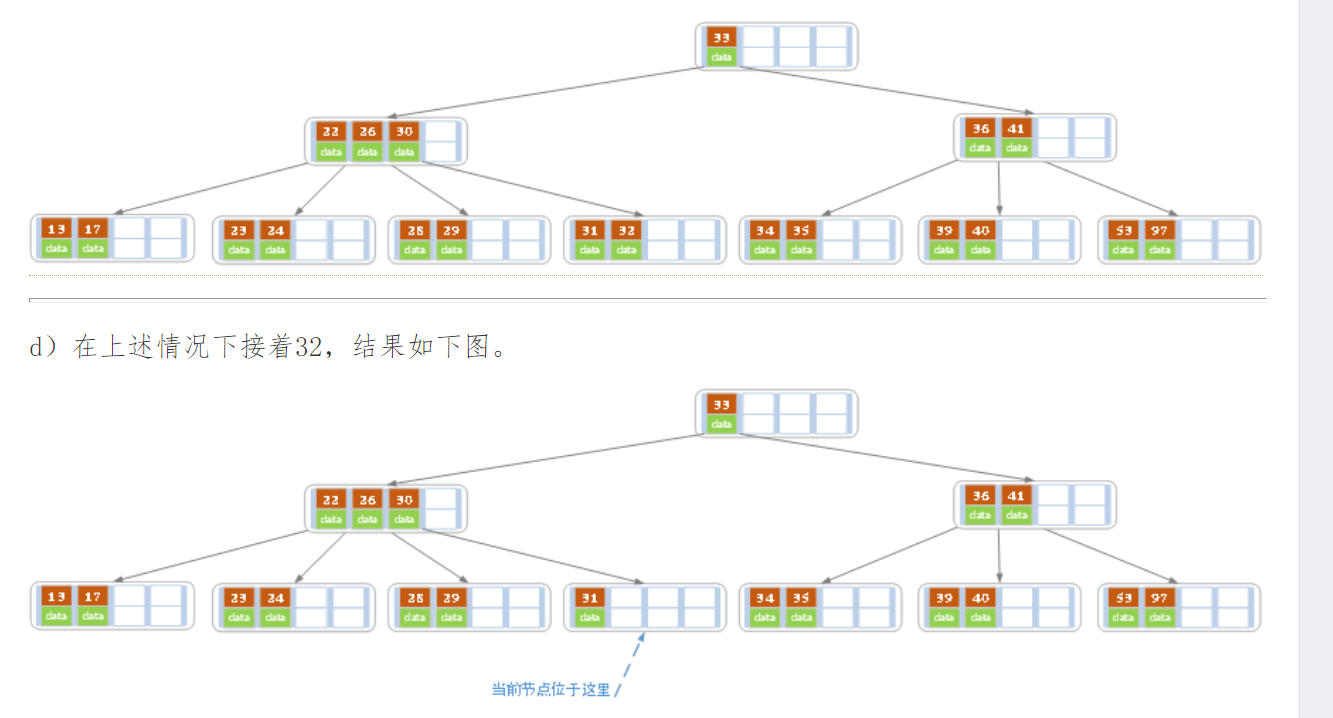

当删除后，当前结点中只key，而兄弟结点中也仅有2个key。
所以只能让父结点中的30下移和这个两个孩子结点中的key合并，成为一个新的结点，当前结点的指针指向父结点。
结果如下图所示。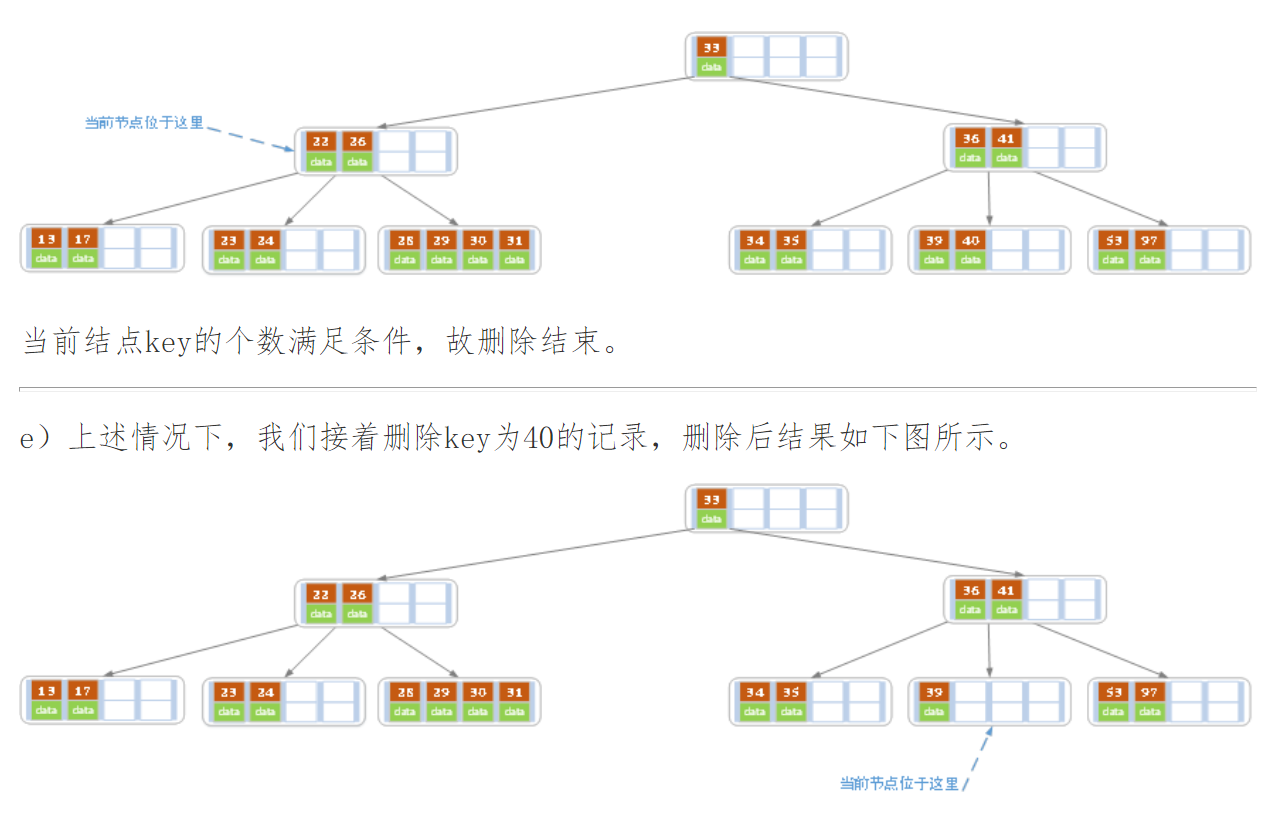

二.B+树

1 B+树的定义

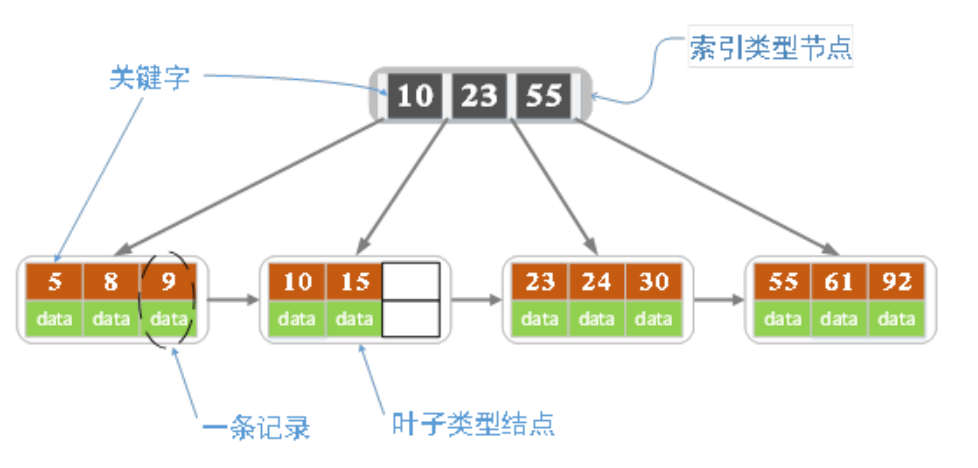
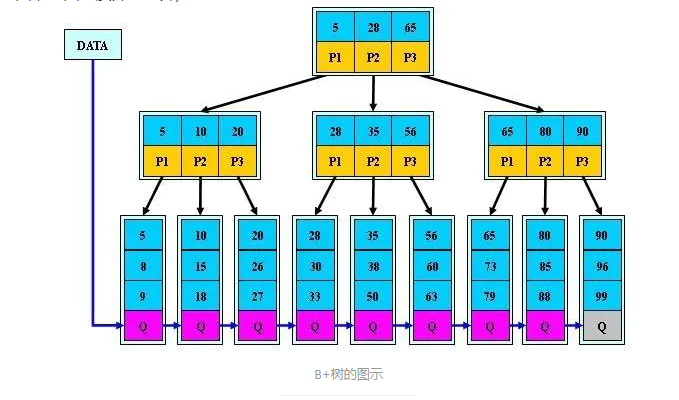
采取维基百科上所定义的方式，即关键字个数比孩子结点个数小1，这种方式是和B树基本等价的。上图就是一颗阶数为4的B+树。
除此之外B+树还有以下的要求。
    1）B+树包含2种类型的结点：内部结点（也称索引结点）和叶子结点。根结点本身即可以是内部结点，也可以是叶子结点。根结点的关键字个数最少可以只有1个。
    2）B+树与B树最大的不同是内部结点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子结点中。
    3） m阶B+树表示了内部结点最多有m-1个关键字（或者说内部结点最多有m个子树），阶数m同时限制了叶子结点最多存储m-1个记录。
    4）内部结点中的key都按照从小到大的顺序排列，对于内部结点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
    5）每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接。

2.B+树的插入操作

1）若为空树，创建一个叶子结点，然后将记录插入其中，此时这个叶子结点也是根结点，插入操作结束。
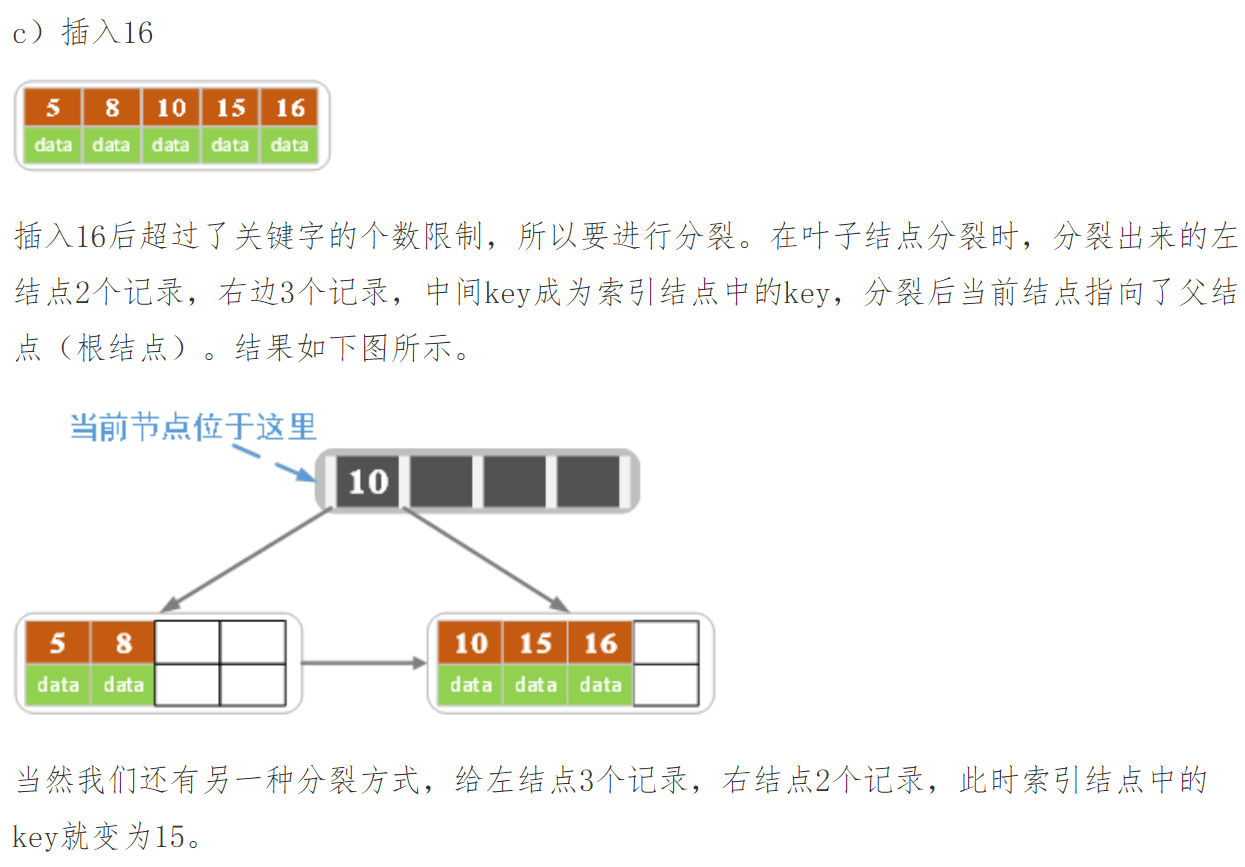
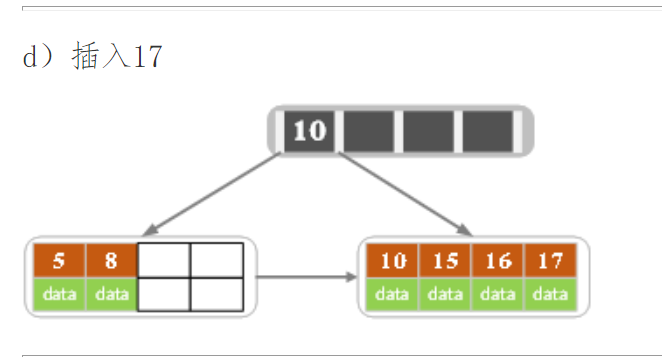
2）针对叶子类型结点：根据key值找到叶子结点，向这个叶子结点插入记录。插入后，若当前结点key的个数小于等于m-1，则插入结束。
    否则将这个叶子结点分裂成左右两个叶子结点，左叶子结点包含前m/2个记录，右结点包含剩下的记录，
    将第m/2+1个记录的key进位到父结点中（父结点一定是索引类型结点），进位到父结点的key左孩子指针向左结点,右孩子指针向右结点。
    将当前结点的指针指向父结点，然后执行第3步。
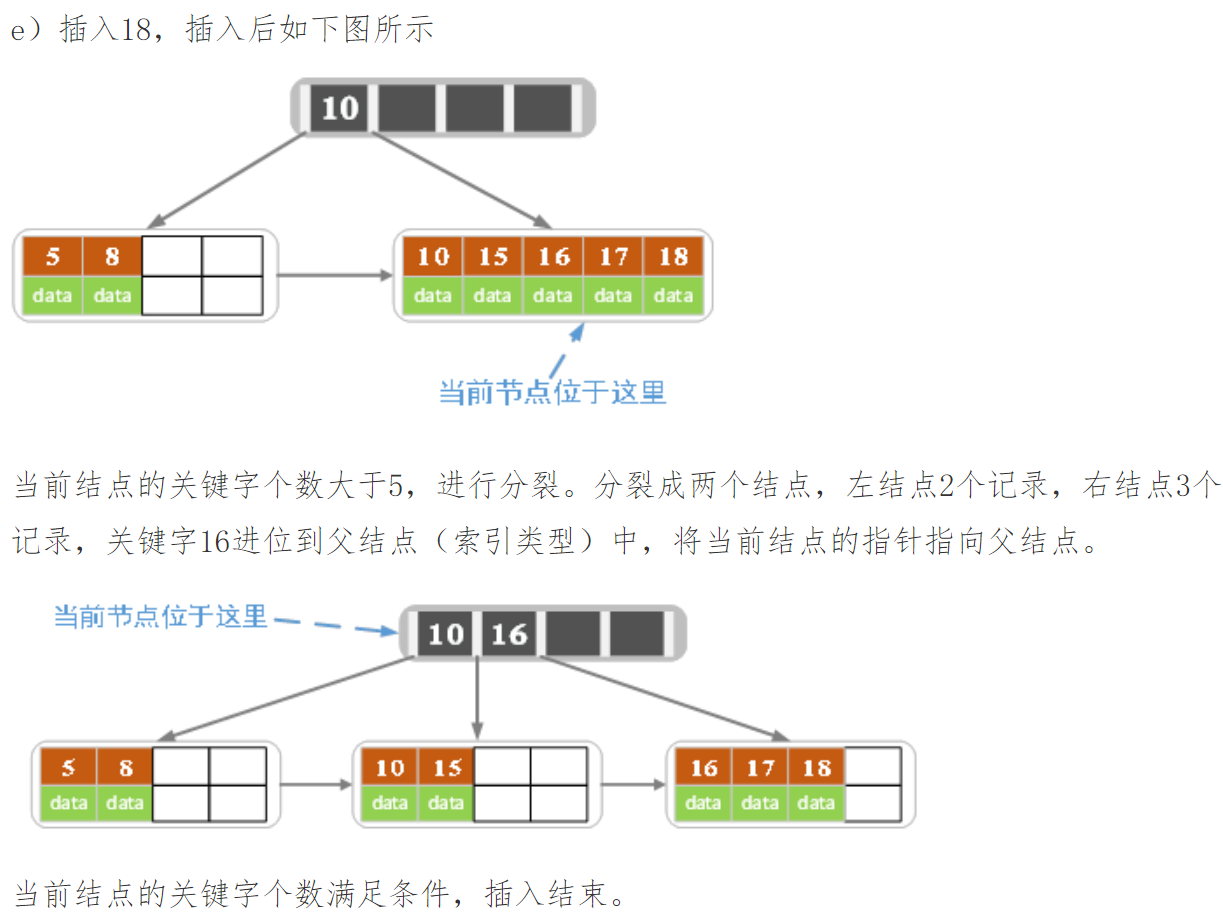
3）针对索引类型结点：若当前结点key的个数小于等于m-1，则插入结束。
    否则，将这个索引类型结点分裂成两个索引结点，左索引结点包含前(m-1)/2个key，右结点包含m-(m-1)/2个key，
    将第m/2个key进位到父结点中，进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。
    将当前结点的指针指向父结点，然后重复第3步。

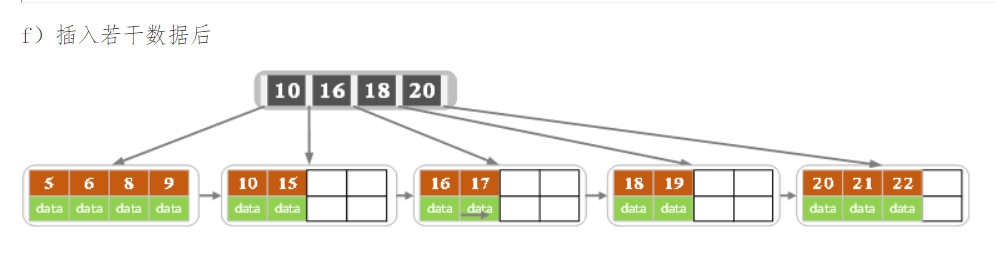
下面是一颗5阶B树的插入过程，5阶B数的结点最少2个key，最多4个key。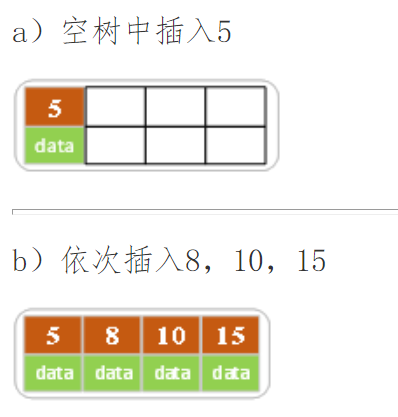

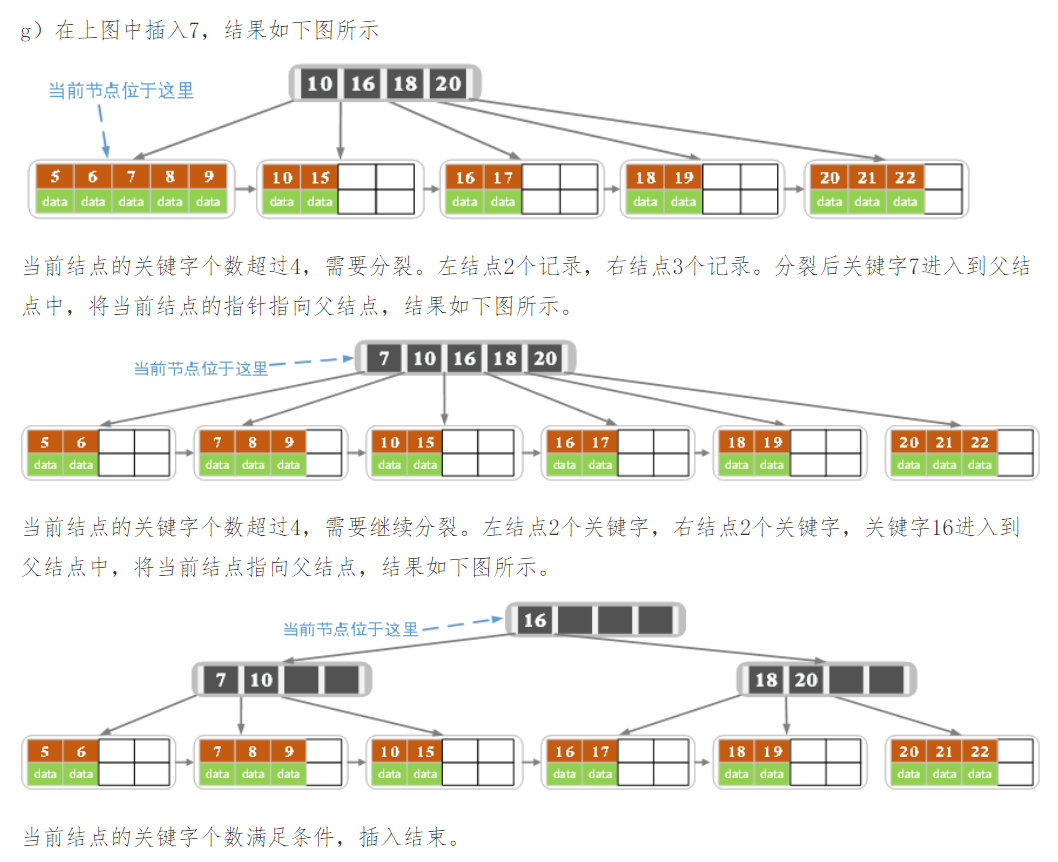
3.B+树的删除操作

如果叶子结点中没有相应的key，则删除失败。否则执行下面的步骤
    1）删除叶子结点中对应的key。删除后若结点的key的个数大于等于Math.ceil(m-1)/2 – 1，删除操作结束,否则执行第2步。
    2）若兄弟结点key有富余（大于Math.ceil(m-1)/2 – 1），向兄弟结点借一个记录，
        同时用借到的key替换父结（指当前结点和兄弟结点共同的父结点）点中的key，删除结束。否则执行第3步。
    3）若兄弟结点中没有富余的key,则当前结点和兄弟结点合并成一个新的叶子结点，并删除父结点中的key（父结点中的这个key两边的孩子指针就变成了一个指针，正好指向这个新的叶子结点）
    ，将当前结点指向父结点（必为索引结点），执行第4步（第4步以后的操作和B树就完全一样了，主要是为了更新索引结点）。
    4）若索引结点的key的个数大于等于Math.ceil(m-1)/2 – 1，则删除操作结束。否则执行第5步
    5）若兄弟结点有富余，父结点key下移，兄弟结点key上移，删除结束。否则执行第6步
    6）当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点，重复第4步。
    注意，通过B+树的删除操作后，索引结点中存在的key，不一定在叶子结点中存在对应的记录。

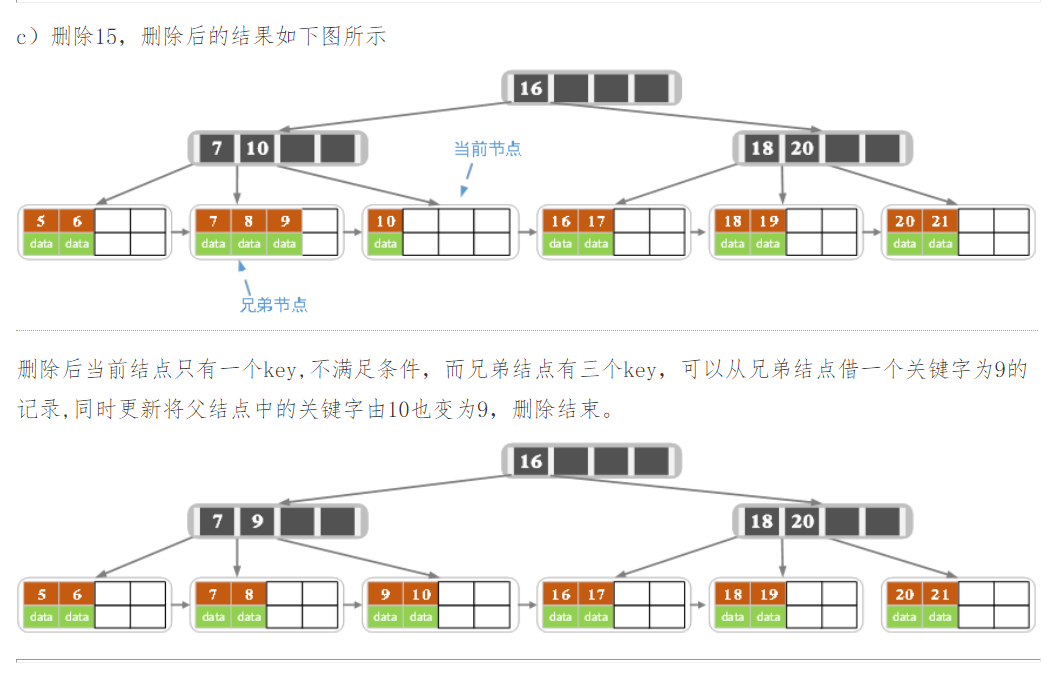
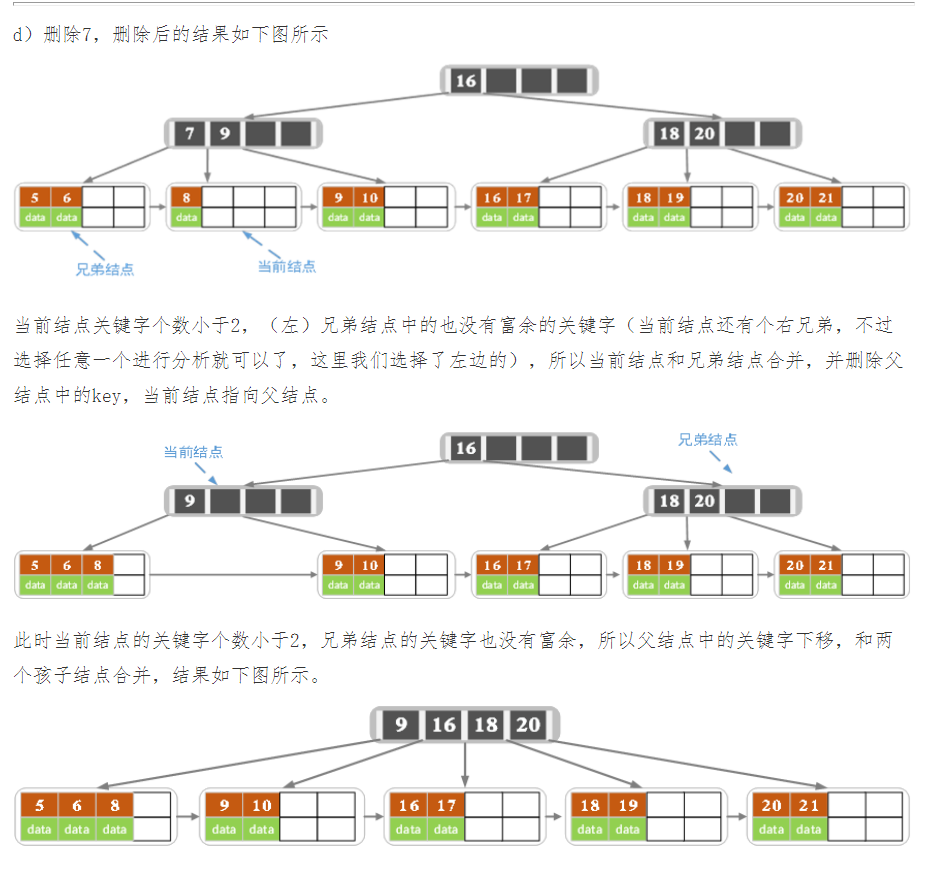
下面是一颗5阶B树的删除过程，5阶B数的结点最少2个key，最多4个key。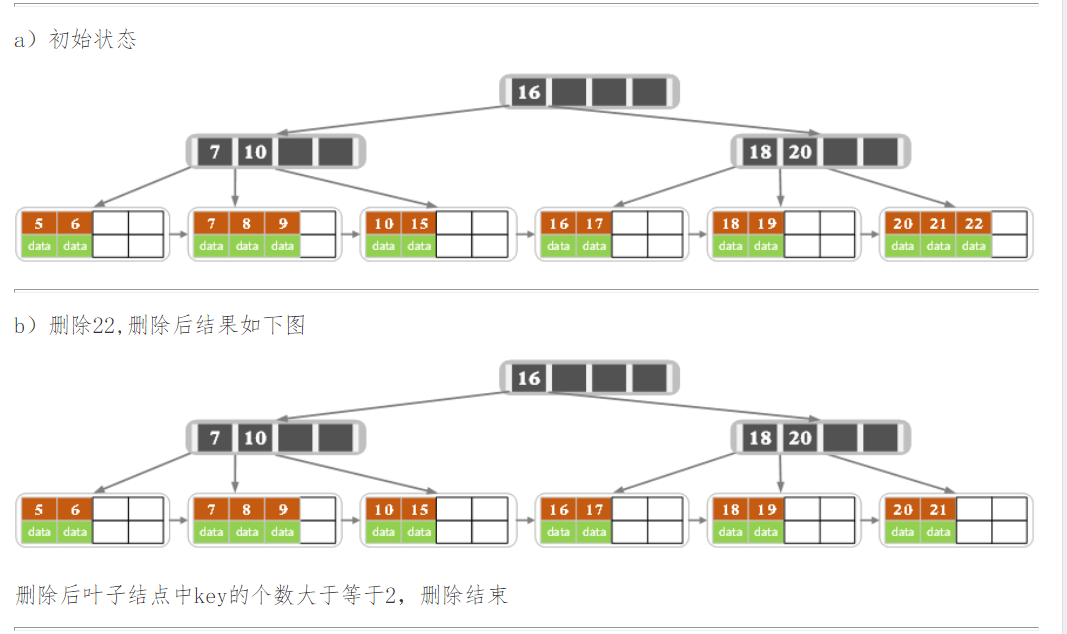

三.B数和B+数

1.B数的使用

(1).B树是为磁盘或其他直接存取的辅助存储设备而设计的一种平衡搜索树。
(2).B树类似于红黑树，但它们在降低磁盘I/O操作数方面要更好一些。现在许多数据库系统使用B树或者B树的变种(B+树和B*树)来存储信息。

2.B+数的使用

(1).B+树是B树的一种变形，它把数据都存储在叶节点中，内部节点只存放关键字和孩子指针.
(2).因此最大化了内部节点的分支因子，所以B+树的遍历也更加高效。

3.B数和B+数遍历

(1).B树需要以中序的方式遍历节点。
(2).B+树只需把所有叶子节点串成链表就可以从头到尾遍历。